En faisant des recherches sur les cours d'Algèbre linéaire, #JaiDécouvert la home page du professeur de #mathématique Bruno Vallette de l'unversité Sorbonne Paris.

Sa "home page" contient beaucoup de ressources, dont :

• un livre nommé L'algèbre linéaire pour tout le monde (lien direct) ;
• et une bande dessinée illustrant l'aventure qu'est la recherche en mathématiques.

En écoutant la vidéo "La réduction de la dimensionnalité (ACP et SVD)", #JaiDécouvert la vidéo "Deux (deux ?) minutes pour l'éléphant de Fermi & Neumann" de la chaine YouTube nommée El Jj (lien direct), à laquelle je viens de m'abonner 🙂.

J'ai été époustouflé par cette vidéo ! Ce qui y est présenté m'impressionne profondément et m'aide à comprendre de nombreuses choses qui m'étaient jusqu'à présent inconnues.

Cette vidéo traite entre autres des Épicycloïde, qui me font penser aux rosaces que je dessinais en école primaire.
Je ne pensais pas que l'étude et l'utilisation de ces courbes étaient aussi intéressantes !

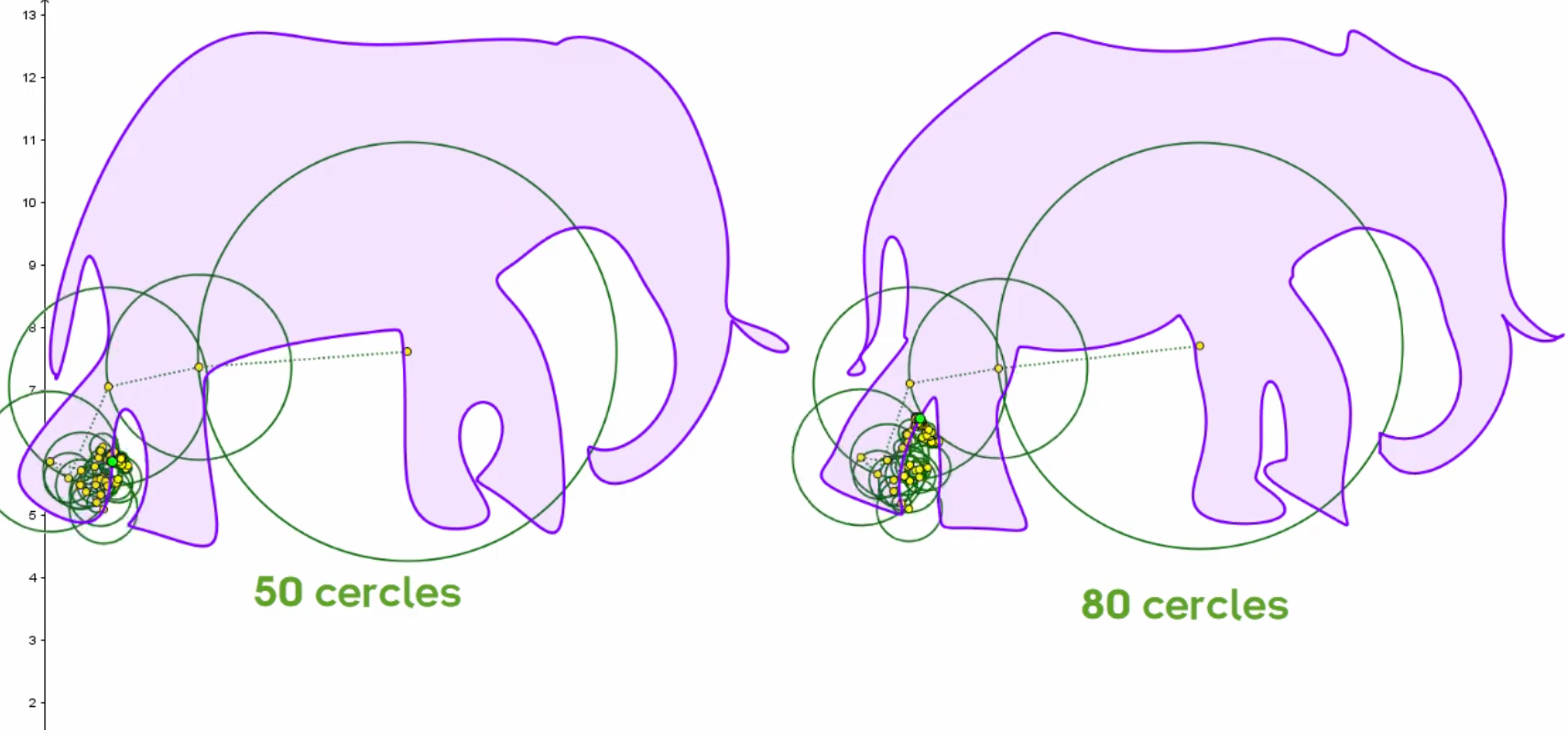
Ce que je retiens :

• Il est possible de représenter n'importe quelle forme avec des épicycloïdes
• Le nombre de cercles permet d'augmenter ou de réduire la précision de la forme, ce qui est utile pour "compresser" le nombre de paramètres nécessaires — avec perte — pour dessiner une forme.

Dans la vidéo, j'ai découvert WolframAlpha (https://www.wolframalpha.com/).
Je n'ai pas réellement compris l'utilité de ce site 😔.
L'article Wikipédia classe ce site dans la catégorie "Moteur de recherche" ou "Base de connaissance" 🤔.

Le pdf : https://www.math.univ-paris13.fr/~vallette/download/ALGLIN.pdf

Un livre du professeur Bruno Vallette.

Article Wikipedia : https://fr.wikipedia.org/wiki/Algèbre_linéaire

Chaine YouTube : https://www.youtube.com/@ElJj

Article Wikipedia : https://fr.wikipedia.org/wiki/Épicycloïde